Complex Logarithm

The complex exponential function generalises the exponential function for complex numbers, and so a natural question is how to generalise to natural logarithm.

However, in the context of complex numbers, the function z↦ez is not injective, since for example

e2πi=e0=1.

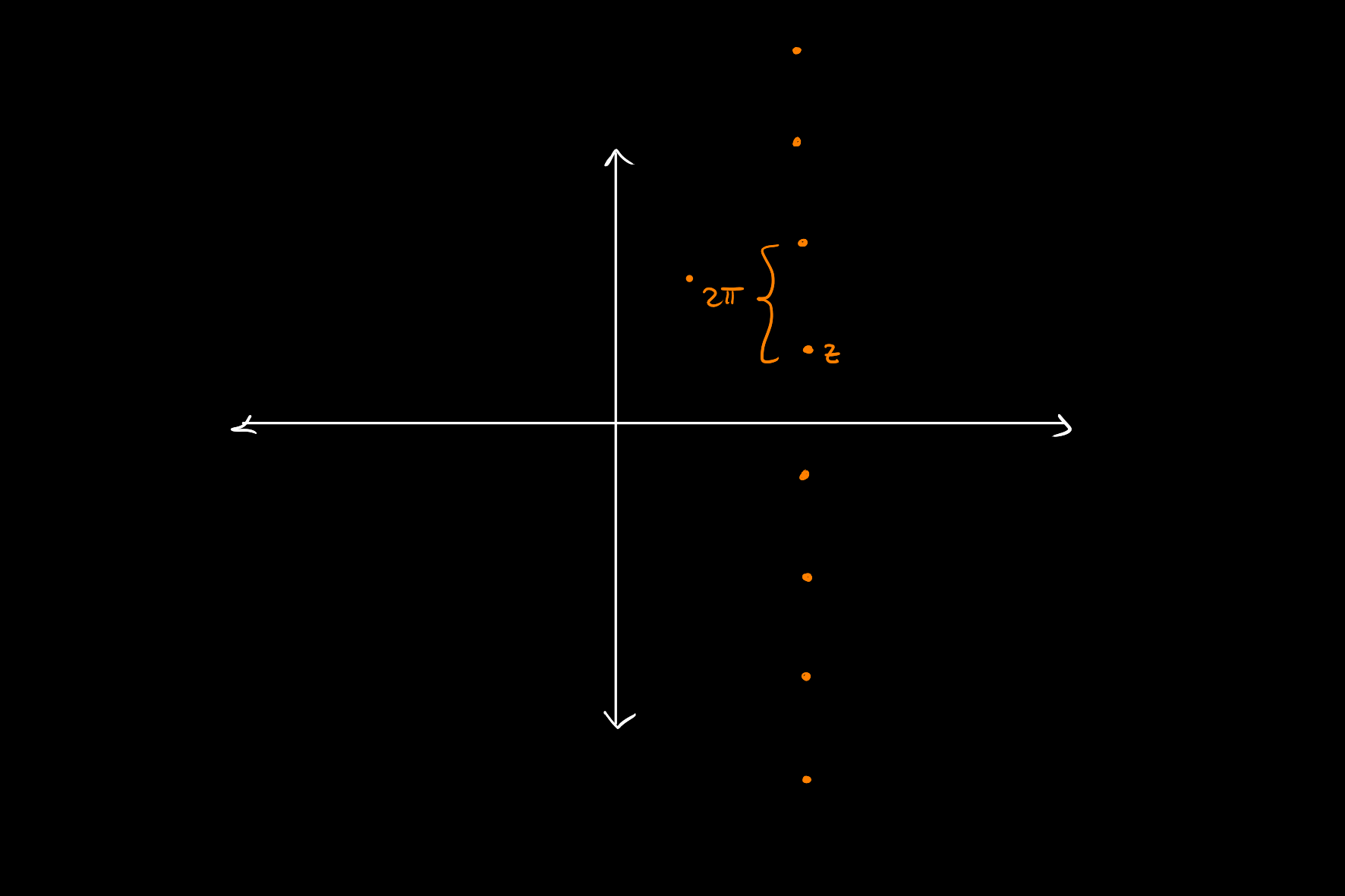
In general, sets of points which differ by a multiple of 2π in the imaginary component get mapped to the same value.

If we ignore this for now, we would naturally say that for a complex number reiθ the logarithm is given by

ln⁡(reiθ)=ln⁡(r)+ln⁡(eiθ)=ln⁡(r)=iθ.

Here the choice of θ would effect the result, so we instead enforce the use of the principal argument. This corresponds with restricting the domain of exp to the region {z∈C:−π<Im(z)≤π}, analagous to the restrictions done for the square root or inverse trigonometric functions.

Definition

For z∈C−{0}

Log(z)=ln⁡(|z|)+iArg(z).

where Arg is the principal argument.

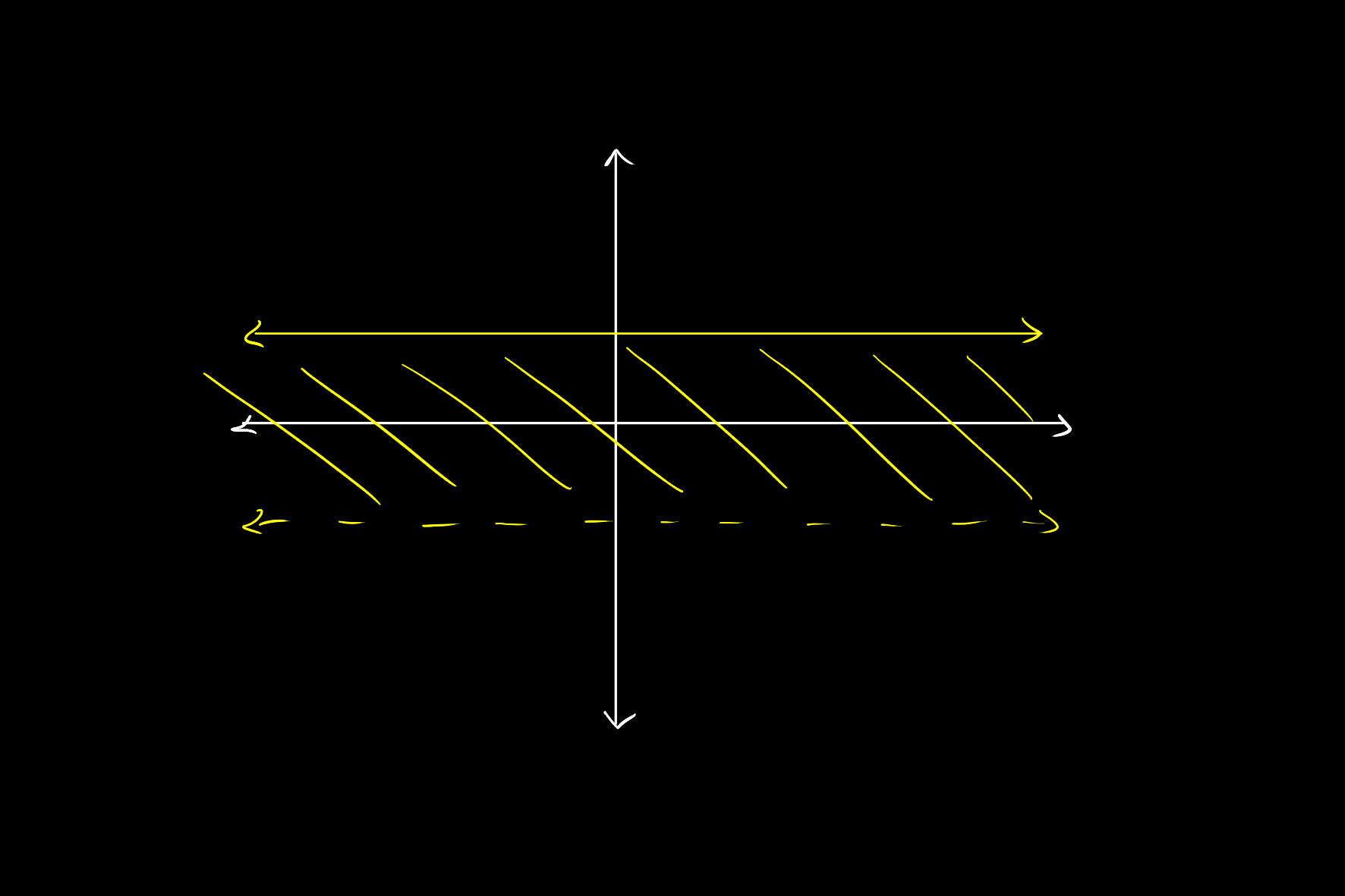
Now we can use this definition to formalise the characterisation of it as in inverse.

Theorem

The function Log as above is an inverse for exp when exp is restricted to the domain {z∈C:−π<Im(z)≤π}.

Corollary

For any z∈C for which the relevant functions are defined

eLog(z)=z

and

Log(ez)=z+2nπi

for some n∈Z.

Definition

For z∈C−{0}

logθ⁡(z)=ln⁡(|z|)+iargθ⁡(z).

With this notation, Log=log−π. Often we call Log the principal branch of the logarithm.